Geometría Analítica
La geometría analítica es una rama de las matemáticas que estudia las figuras, sus distancias, sus áreas, puntos de intersección, ángulos de inclinación, puntos de división, volúmenes, etcétera. Analiza con detalle los datos de las figuras geométricas mediante técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas. Su desarrollo histórico comienza con la geometría cartesiana, continúa con la aparición de la geometría diferencial de Carl Friedrich Gauss y más tarde con el desarrollo de la geometría algebraica. Tiene múltiples aplicaciones, más allá de las matemáticas y la ingeniería, pues forma parte ahora del trabajo de administradores para la planeación de estrategias y logística en la toma de decisiones.
Gráfica de dos hipérbolas y sus asíntotas.
Las dos cuestiones fundamentales de la geometría analítica son:
Dado el lugar geométrico de un sistema de coordenadas, para obtener su ecuación.
Dada la ecuación en un sistema de coordenadas, determinar la gráfica o lugar geométrico de los puntos que verifican dicha ecuación.
La geometría analítica representa las figuras geométricas mediante la ecuación y=f(x)}
, donde f}
es una función u otro tipo. Así, las rectas se expresan mediante la ecuación general ax+by=c}
, las circunferencias y el resto de cónicas como ecuaciones polinómicas de grado 2 (la circunferencia, x^{2}+y^{2}=4}
; la hipérbola, xy=1}
).
El matemático griego Menecmo resolvió problemas y demostró teoremas utilizando un método que tenía un gran parecido con el uso de coordenadas y, en ocasiones, se ha sostenido que había introducido la geometría analítica.1
1. Apolonio de Perge, en Sobre la sección determinada, trató los problemas de una manera que puede llamarse geometría analítica de una dimensión; con la cuestión de encontrar puntos en una recta que estuvieran en proporción a los demás.
7. Europa Occidental
La geometría analítica fue inventada de forma independiente por René Descartes y Pierre de Fermat,89 aunque a Descartes a veces se le da el crédito exclusivo.1011 La geometría cartesiana, el término alternativo utilizado para la geometría analítica, lleva el nombre de Descartes.
Descartes hizo un progreso significativo con los métodos en un ensayo titulado La Géométrie (La Geometría), uno de los tres ensayos adjuntos (apéndices) publicados en 1637 junto con su Discurso sobre el método para dirigir correctamente la razón y buscar la verdad en las ciencias, comúnmente denominado Discurso del método. La Géométrie, escrita en su lengua materna francesa, y sus principios filosóficos, sirvieron de base para el cálculo en Europa. Inicialmente, el trabajo no fue bien recibido debido, en parte, a las muchas lagunas en los argumentos y ecuaciones complicadas. Sólo después de la traducción al latín y la adición de comentarios por Frans van Schooten en 1649 (y otros trabajos posteriores) hizo que la obra maestra de Descartes recibiera el debido reconocimiento.12
Pierre de Fermat también fue pionero en el desarrollo de la geometría analítica. Aunque no se publicó durante su vida, una forma manuscrita de Ad locos planos et solidos isagoge (Introducción a los lugares planos y sólidos) circulaba en París en 1637, justo antes de la publicación del Discurso de Descartes.131415 Claramente escrita y bien recibida, la Introducción También sentó las bases para la geometría analítica. La diferencia clave entre los tratamientos de Fermat y Descartes es una cuestión de punto de vista: Fermat siempre comenzaba con una ecuación algebraica y luego describía la curva geométrica que la satisfacía, mientras que Descartes comenzaba con curvas geométricas y producía sus ecuaciones como una de varias propiedades de las curvas.12 Como consecuencia de este enfoque, Descartes tuvo que lidiar con ecuaciones más complicadas y tuvo que desarrollar los métodos para trabajar con ecuaciones polinómicas de mayor grado. Fue Leonhard Euler quien aplicó por primera vez el método de coordenadas en un estudio sistemático de superficies y curvas espaciales.
Construcciones fundamentales.
En un sistema de coordenadas cartesianas, un punto del plano queda determinado por dos números, llamados abscisa y ordenada del punto. Mediante ese procedimiento a todo punto del plano corresponden siempre dos números reales ordenados (abscisa y ordenada), y recíprocamente, a un par ordenado de números corresponde un único punto del plano. Consecuentemente el sistema cartesiano establece una correspondencia biunívoca entre un concepto geométrico como es el de los puntos del plano y un concepto algebraico como son los pares ordenados de números. Esta correspondencia constituye el fundamento de la geometría analítica.
Con la geometría analítica se puede determinar figuras geométricas planas por medio de ecuaciones e inecuaciones con dos incógnitas. Este es un método alternativo de resolución de problemas, o cuando menos nos proporciona un nuevo punto de vista con el cual poder atacar el problema.
Localización de un punto en el plano cartesiano
Dada la ecuación en un sistema de coordenadas, determinar la gráfica o lugar geométrico de los puntos que verifican dicha ecuación.
La geometría analítica representa las figuras geométricas mediante la ecuación y=f(x)}
, donde f} es una función u otro tipo. Así, las rectas se expresan mediante la ecuación general ax+by=c}, las circunferencias y el resto de cónicas como ecuaciones polinómicas de grado 2 (la circunferencia, x^{2}+y^{2}=4}; la hipérbola, xy=1}). Historia
El matemático griego Menecmo resolvió problemas y demostró teoremas utilizando un método que tenía un gran parecido con el uso de coordenadas y, en ocasiones, se ha sostenido que había introducido la geometría analítica.1
1. Apolonio de Perge, en Sobre la sección determinada, trató los problemas de una manera que puede llamarse geometría analítica de una dimensión; con la cuestión de encontrar puntos en una recta que estuvieran en proporción a los demás.
2 . Apolonio en las Cónicas desarrolló además un método que es tan similar a la geometría analítica que a veces se piensa que su trabajo se anticipó al trabajo de Descartes por unos 1800 años. Su aplicación de líneas de referencia, un diámetro y una tangente no es esencialmente diferente de nuestro uso moderno de un marco de coordenadas, donde las distancias medidas a lo largo del diámetro desde el punto de tangencia son las abscisas, y los segmentos paralelos a la tangente e interceptados entre el eje y la curva son las ordenadas. Desarrolló además relaciones entre las abscisas y las ordenadas correspondientes que son equivalentes a ecuaciones retóricas (expresadas en palabras) de curvas. Sin embargo, aunque Apolonio estuvo cerca de desarrollar la geometría analítica, no lo logró ya que no tuvo en cuenta las magnitudes negativas y en todos los casos el sistema de coordenadas se superpuso a una curva dada a posteriori en lugar de a priori. Es decir, las ecuaciones estaban determinadas por curvas, pero las curvas no estaban determinadas por ecuaciones. Las coordenadas, las variables y las ecuaciones eran nociones subsidiarias aplicadas a una situación geométrica específica.
Persia[editar]
3. El matemático persa del siglo XI Omar Jayam vio una fuerte relación entre la geometría y el álgebra y se estaba moviendo en la dirección correcta cuando ayudó a cerrar la brecha entre el álgebra numérica
Persia[editar]
3. El matemático persa del siglo XI Omar Jayam vio una fuerte relación entre la geometría y el álgebra y se estaba moviendo en la dirección correcta cuando ayudó a cerrar la brecha entre el álgebra numérica
4 y geométrica con su solución geométrica de las ecuaciones cúbicas generales,
5 pero el paso decisivo vino después con Descartes. A Omar Jayam se le atribuye la identificación de los fundamentos de la geometría algebraica, y su libro Tratado sobre demostraciones de problemas de álgebra (1070), que estableció los principios de la geometría analítica, es parte del cuerpo de matemáticas persas que finalmente se transmitió. a Europa.
6 Debido a su enfoque geométrico completo de las ecuaciones algebraicas, Jayampuede considerarse un precursor de Descartes en la invención de la geometría analítica.
7. Europa Occidental
La geometría analítica fue inventada de forma independiente por René Descartes y Pierre de Fermat,89 aunque a Descartes a veces se le da el crédito exclusivo.1011 La geometría cartesiana, el término alternativo utilizado para la geometría analítica, lleva el nombre de Descartes.
Descartes hizo un progreso significativo con los métodos en un ensayo titulado La Géométrie (La Geometría), uno de los tres ensayos adjuntos (apéndices) publicados en 1637 junto con su Discurso sobre el método para dirigir correctamente la razón y buscar la verdad en las ciencias, comúnmente denominado Discurso del método. La Géométrie, escrita en su lengua materna francesa, y sus principios filosóficos, sirvieron de base para el cálculo en Europa. Inicialmente, el trabajo no fue bien recibido debido, en parte, a las muchas lagunas en los argumentos y ecuaciones complicadas. Sólo después de la traducción al latín y la adición de comentarios por Frans van Schooten en 1649 (y otros trabajos posteriores) hizo que la obra maestra de Descartes recibiera el debido reconocimiento.12
Pierre de Fermat también fue pionero en el desarrollo de la geometría analítica. Aunque no se publicó durante su vida, una forma manuscrita de Ad locos planos et solidos isagoge (Introducción a los lugares planos y sólidos) circulaba en París en 1637, justo antes de la publicación del Discurso de Descartes.131415 Claramente escrita y bien recibida, la Introducción También sentó las bases para la geometría analítica. La diferencia clave entre los tratamientos de Fermat y Descartes es una cuestión de punto de vista: Fermat siempre comenzaba con una ecuación algebraica y luego describía la curva geométrica que la satisfacía, mientras que Descartes comenzaba con curvas geométricas y producía sus ecuaciones como una de varias propiedades de las curvas.12 Como consecuencia de este enfoque, Descartes tuvo que lidiar con ecuaciones más complicadas y tuvo que desarrollar los métodos para trabajar con ecuaciones polinómicas de mayor grado. Fue Leonhard Euler quien aplicó por primera vez el método de coordenadas en un estudio sistemático de superficies y curvas espaciales.
Construcciones fundamentales.
En un sistema de coordenadas cartesianas, un punto del plano queda determinado por dos números, llamados abscisa y ordenada del punto. Mediante ese procedimiento a todo punto del plano corresponden siempre dos números reales ordenados (abscisa y ordenada), y recíprocamente, a un par ordenado de números corresponde un único punto del plano. Consecuentemente el sistema cartesiano establece una correspondencia biunívoca entre un concepto geométrico como es el de los puntos del plano y un concepto algebraico como son los pares ordenados de números. Esta correspondencia constituye el fundamento de la geometría analítica.
Con la geometría analítica se puede determinar figuras geométricas planas por medio de ecuaciones e inecuaciones con dos incógnitas. Este es un método alternativo de resolución de problemas, o cuando menos nos proporciona un nuevo punto de vista con el cual poder atacar el problema.
Localización de un punto en el plano cartesiano
Como distancia a los ejes
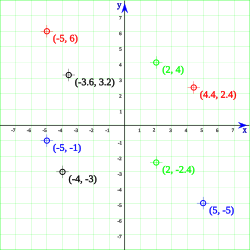
Ejemplos de ocho puntos localizados en el plano cartesiano mediante sus pares de coordenadas.
En un plano (v.g. papel milimetrado) se traza dos rectas orientadas perpendiculares entre sí (ejes) —que por convenio se trazan de manera que una de ellas sea horizontal y la otra vertical—, y cada punto del plano queda unívocamente determinado por las distancias de dicho punto a cada uno de los ejes, siempre y cuando se dé también un criterio para determinar sobre qué semiplano determinado por cada una de las rectas hay que tomar esa distancia, criterio que viene dado por un signo. Ese par de números, las coordenadas, quedará representado por un par ordenado (x,y)}
, siendo 
la distancia a uno de los ejes (por convenio será la distancia al eje vertical) 
la distancia al otro eje (al horizontal).
En la coordenada, el signo positivo (que suele omitirse) significa que la distancia se toma hacia la derecha sobre el eje horizontal (eje de las abscisas), y el signo negativo (nunca se omite) indica que la distancia se toma hacia la izquierda. Para la coordenada , el signo positivo (también se omite) indica que la distancia se toma hacia arriba sobre el eje vertical (eje de ordenadas), tomándose hacia abajo si el signo es negativo (en ningún caso se omiten los signos negativos).
A la coordenada se la suele denominar abscisa del punto, mientras que a la se la denomina ordenada del punto.
Los puntos del eje de abscisas tienen por lo tanto ordenada igual a
, así que serán de la 
, mientras que los del eje de ordenadas tendrán abscisa igual a , por lo que serán de la forma 
.
El punto donde ambos ejes se cruzan tendrá por lo tanto distancia a cada uno de los ejes, luego su abscisa será y su ordenada también será . A este punto —el 
— se le denomina origen de coordenadas.
Como proyección sobre los ejes.
Coordenadas asignadas a tres puntos diferentes (verde, rojo y azul), sus proyecciones ortogonales sobre los ejes constituyen sus coordenadas cartesianas.
Se consideran dos rectas orientadas, (ejes), perpendiculares entre sí, "x" e "y", con un origen común, el punto O de intersección de ambas rectas.
Teniendo un punto a, al cual se desea determinar las coordenadas, se procede de la siguiente forma:
Por el punto P se trazan rectas perpendiculares a los ejes, éstas determinan en la intersección con los mismos dos puntos, P' (el punto ubicado sobre el eje x) y el punto P'' ( el punto ubicado sobre el eje y).
Dichos puntos son las proyecciones ortogonales sobre los ejes x e y del punto P.
A los Puntos P' y P'' le corresponden por número la distancia desde ellos al origen, teniendo en cuenta que si el punto P' se encuentra a la izquierda de O, dicho número será negativo, y si el punto P'' se encuentra por debajo del punto O, dicho número será negativo.
Los números relacionados con P' y P'', en ese orden son los valores de las coordenadas del punto P.
Ejemplo 1: P' se encuentra a la derecha de O una distancia igual a 2 unidades. P'' se encuentra hacia arriba de O, una distancia igual a 3 unidades. Por lo que las coordenadas de P son (2, 3).
Ejemplo 2: P' se encuentra a la derecha de O una distancia igual a 4 unidades. P'' se encuentra hacia abajo de O, una distancia igual a 5 unidades. Por lo que las coordenadas de P son (4, -5).
Ejemplo 3: P' se encuentra a la izquierda de O una distancia igual a 3 unidades. P'' se encuentra hacia abajo de O, una distancia igual a 2 unidades. Por lo que las coordenadas de P son (-3, -2).
Ejemplo 4: P' se encuentra a la izquierda de O una distancia igual a 6 unidades. P'' se encuentra hacia arriba de O, una distancia igual a 4 unidades. Por lo que las coordenadas de P son (-6, 4).
Ecuaciones de la recta en el plano
Artículo principal: Función lineal
Una recta es el lugar geométrico de todos los puntos en el plano tales que, tomados dos cualesquiera de ellos, el cálculo de la pendiente resulta siempre igual a una constante.
La ecuación general de la recta es de la forma:
Ax+By+C=0\,}
cuya pendiente es m = -A/B y cuya ordenada al origen es b = -C/B.
Una recta en el plano se representa con la función lineal de la forma:
Como expresión general, ésta es conocida con el nombre de ecuación pendiente-ordenada al origen y podemos distinguir dos casos particulares. Si una recta no corta a uno de los ejes, será porque es paralela a él. Como los dos ejes son perpendiculares, si no corta a uno de ellos forzosamente ha de cortar al otro (siempre y cuando la función sea continua para todos los reales). Tenemos pues tres casos:
Ejemplos de ocho puntos localizados en el plano cartesiano mediante sus pares de coordenadas.
En un plano (v.g. papel milimetrado) se traza dos rectas orientadas perpendiculares entre sí (ejes) —que por convenio se trazan de manera que una de ellas sea horizontal y la otra vertical—, y cada punto del plano queda unívocamente determinado por las distancias de dicho punto a cada uno de los ejes, siempre y cuando se dé también un criterio para determinar sobre qué semiplano determinado por cada una de las rectas hay que tomar esa distancia, criterio que viene dado por un signo. Ese par de números, las coordenadas, quedará representado por un par ordenado (x,y)}
, siendo la distancia a uno de los ejes (por convenio será la distancia al eje vertical) la distancia al otro eje (al horizontal).En la coordenada
, el signo positivo (que suele omitirse) significa que la distancia se toma hacia la derecha sobre el eje horizontal (eje de las abscisas), y el signo negativo (nunca se omite) indica que la distancia se toma hacia la izquierda. Para la coordenada , el signo positivo (también se omite) indica que la distancia se toma hacia arriba sobre el eje vertical (eje de ordenadas), tomándose hacia abajo si el signo es negativo (en ningún caso se omiten los signos negativos).A la coordenada
se la suele denominar abscisa del punto, mientras que a la se la denomina ordenada del punto.Los puntos del eje de abscisas tienen por lo tanto ordenada igual a
, así que serán de la , mientras que los del eje de ordenadas tendrán abscisa igual a , por lo que serán de la forma .El punto donde ambos ejes se cruzan tendrá por lo tanto distancia
a cada uno de los ejes, luego su abscisa será y su ordenada también será . A este punto —el — se le denomina origen de coordenadas.Como proyección sobre los ejes.
Coordenadas asignadas a tres puntos diferentes (verde, rojo y azul), sus proyecciones ortogonales sobre los ejes constituyen sus coordenadas cartesianas.
Se consideran dos rectas orientadas, (ejes), perpendiculares entre sí, "x" e "y", con un origen común, el punto O de intersección de ambas rectas.
Teniendo un punto a, al cual se desea determinar las coordenadas, se procede de la siguiente forma:
Por el punto P se trazan rectas perpendiculares a los ejes, éstas determinan en la intersección con los mismos dos puntos, P' (el punto ubicado sobre el eje x) y el punto P'' ( el punto ubicado sobre el eje y).
Dichos puntos son las proyecciones ortogonales sobre los ejes x e y del punto P.
A los Puntos P' y P'' le corresponden por número la distancia desde ellos al origen, teniendo en cuenta que si el punto P' se encuentra a la izquierda de O, dicho número será negativo, y si el punto P'' se encuentra por debajo del punto O, dicho número será negativo.
Los números relacionados con P' y P'', en ese orden son los valores de las coordenadas del punto P.
Ejemplo 1: P' se encuentra a la derecha de O una distancia igual a 2 unidades. P'' se encuentra hacia arriba de O, una distancia igual a 3 unidades. Por lo que las coordenadas de P son (2, 3).
Ejemplo 2: P' se encuentra a la derecha de O una distancia igual a 4 unidades. P'' se encuentra hacia abajo de O, una distancia igual a 5 unidades. Por lo que las coordenadas de P son (4, -5).
Ejemplo 3: P' se encuentra a la izquierda de O una distancia igual a 3 unidades. P'' se encuentra hacia abajo de O, una distancia igual a 2 unidades. Por lo que las coordenadas de P son (-3, -2).
Ejemplo 4: P' se encuentra a la izquierda de O una distancia igual a 6 unidades. P'' se encuentra hacia arriba de O, una distancia igual a 4 unidades. Por lo que las coordenadas de P son (-6, 4).
Ecuaciones de la recta en el plano
Artículo principal: Función lineal
Una recta es el lugar geométrico de todos los puntos en el plano tales que, tomados dos cualesquiera de ellos, el cálculo de la pendiente resulta siempre igual a una constante.
La ecuación general de la recta es de la forma:
Ax+By+C=0\,}
cuya pendiente es m = -A/B y cuya ordenada al origen es b = -C/B.
Una recta en el plano se representa con la función lineal de la forma:
Como expresión general, ésta es conocida con el nombre de ecuación pendiente-ordenada al origen y podemos distinguir dos casos particulares. Si una recta no corta a uno de los ejes, será porque es paralela a él. Como los dos ejes son perpendiculares, si no corta a uno de ellos forzosamente ha de cortar al otro (siempre y cuando la función sea continua para todos los reales). Tenemos pues tres casos:
video de la geometría analítica
Ana Patricia Centeno Sorto
ResponderEliminar