REFLEXION:
DEFINCION:
En esta temática se estudiará muy concienzudamente la expresión ![]() conocida como la enésima potencia de a.
conocida como la enésima potencia de a.
Definición 1
Para n número natural y a número real se define la n- Potencia de a como el producto de a por si misma n- veces; es decir, ![]() . El número a se conoce como la base y n como el exponente.
. El número a se conoce como la base y n como el exponente.
iniciará el estudio de la expresión ![]() en el caso donde a represente cualquier número real, es decir, a ∈ R y n un número entero positivo (
en el caso donde a represente cualquier número real, es decir, a ∈ R y n un número entero positivo ( ![]() ), para este primer caso, la definición no presenta ninguna dificultad.
), para este primer caso, la definición no presenta ninguna dificultad.
Ejemplos 1
Otro Ejemplo: ![]() para el ejemplo
para el ejemplo ![]() . Para este caso, la base de la potencia es (-2) que difiere de
. Para este caso, la base de la potencia es (-2) que difiere de ![]() donde la base es 2 y el signo menos es un factor de la potencia.
donde la base es 2 y el signo menos es un factor de la potencia.
El comportamiento de los exponentes en las operaciones con potencias está gobernado por ciertas reglas sencillas, pero se debe estar muy atento al aplicarlas con el fin de no caer en errores que van en contra de la definición.
PRODUCTO DE POTENCIAS DE IGUAL BASE.
Al efectuar productos de potencias de igual base se obtiene como resultado una potencia de igual base y como exponente la suma de los exponentes de las potencias involucradas, es decir: ![]() .
.
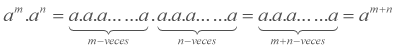
COCIENTE DE POTENCIAS DE IGUAL BASE.
Al efectuar cocientes de potencias de igual base se obtiene como resultado una potencia de igual base y como exponente la resta de los exponentes de las potencias involucradas, es decir: 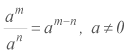 .
.
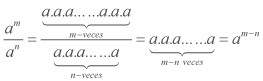
POTENCIA DE UNA POTENCIA.
Al elevar una potencia a una nueva potencia, se obtiene como resultado una potencia con la misma base, y como exponente el producto de los exponentes involucrados, es decir: ![]() .
.

POTENCIA CUYA BASE ES UN PRODUCTO.
Cuando se tiene una potencia cuya base es un producto de dos o más factores, se puede distribuir el exponente en cada una de los factores, es decir: ![]() .
.
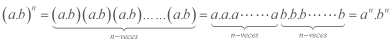
Aplicando conmutativa y asociativa tantas veces como sea necesario.
POTENCIA CUYA BASE ES UN COCIENTE
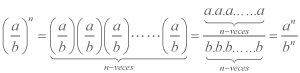
Cuando se tiene una potencia cuya base es un cociente de dos o más factores, se puede distribuir el exponente en cada una de los factores, es decir: 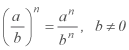 .
.
Ejemplo 2
Utilizar las reglas de los exponentes para simplificar cada una de las siguientes expresiones y después calcular su resultado.
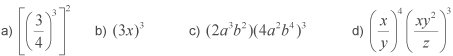
Solución:
En este ejemplo también se puede iniciar utilizando primero la propiedad de potencia cuya base es un cociente y luego la regla de potencia de una potencia.
Hasta el momento en la definición de la n-esima Potencia de a , es decir, ![]() el conjunto donde toma valores a son los números reales y donde toma valores n son los enteros positivos o los números naturales.
el conjunto donde toma valores a son los números reales y donde toma valores n son los enteros positivos o los números naturales.




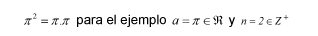


Comentarios
Publicar un comentario