REFLEXION:
Proporcionalidad simple directa e inversa
Introducción
Proporcionalidad directa:
Dos magnitudes y son directamente proporcionales cuando existe una constante tal que
La constante se denomina constante de proporcionalidad o razón.
Se dice que y mantienen una relación de proporcionalidad directa.
En este tipo de proporcionalidad, cuando una de las magnitudes aumenta, la otra también; y lo mismo ocurre cuando alguna de las dos disminuye.
Ejemplo:
En un movimiento con velocidad constante , la distancia recorrida viene dada por la ecuación
La distancia es directamente proporcional al tiempo puesto que
En este ejemplo, la velocidad es la constante de proporcionalidad.
Cuando el tiempo aumenta, la distancia también lo hace y viceversa.
Regla de tres (directa)
Si dos magnitudes y mantienen una relación de proporcionalidad directa, una regla de tres simple directa (o simplemente regla de tres directa) nos permite conocer el valor de una de las dos magnitudes cuando la otra varía.
Para aplicar una regla de tres, escribimos la siguiente tabla:
+ | Valor | Valor |
Magnitud | ||
Magnitud |
Como la relación de proporcionalidad directa debe ser constante, ha de cumplirse que
De esta relación podemos despejar el valor que deseamos calcular.
Proporcionalidad inversa:
Dos magnitudes y son inversamente proporcionales cuando existe una constante tal que
La constante se denomina constante de proporcionalidad.
En esta proporcionalidad, cuando una de las magnitudes aumenta, la otra disminuye y viceversa.
Ejemplo:
Si un trabajador pinta una valla en 10 horas, entonces para pintar la misma valla entre dos trabajadores se necesitan 5 horas.
Se trata de una proporcionalidad inversa puesto que cuando aumenta el número de trabajadores, el número de horas necesarias disminuye. La constante de proporcionalidad es 10 porque
Es decir, si es el número de trabajadores y el número de horas, entonces
Regla de tres (inversa)
Cuando dos magnitudes y mantienen una relación de proporcionalidad inversa, una regla de tres simple inversa (o simplemente regla de tres inversa) nos permite conocer el valor de una de las dos magnitudes cuando la otra varía.
Para aplicar una regla de tres, escribimos la siguiente tabla:
- | Valor | Valor |
Magnitud | ||
Magnitud |
Como la relación de proporcionalidad indirecta debe ser constante, se cumple que
De esta relación podemos despejar el valor que deseamos calcular.
Nota: en ocasiones se utilizan los signos (+) y (-) en las tablas escritas anteriormente para denotar que se trata de una proporcionalidad directa e indirecta, respectivamente.
Problema 1
Calcular la razón de los números
15 y 25
12 y 32
3 y 81
30 y 40
111 y 33
La razón es el cociente de los números. Escribiremos los números como productos para simplificar las fracciones rápidamente
15 y 20
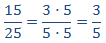
12 y 32
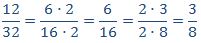
3 y 81
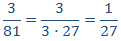
30 y 40
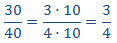
111 y 33
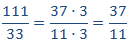




Comentarios
Publicar un comentario